Zem je guľatá. Teda vlastne takmer guľatá.
Tvar Zeme najpresnejšie vystihuje geoid – teleso, ktoré je podobné guli s malým sploštením v oblasti pólov. Logicky najvhodnejšie je ale zobrazovať zemský povrch na guľu. Zmenšeným modelom Zeme je glóbus, ktorý vo všeobecnosti zachováva veľkosti uhlov aj vzdialeností v danej mierke.
Tam kde nie je možné používať glóbus – predsa len, nie je obvykle vo vreckovej forme – tam prichádza na scénu mapa. A tá je obvykle plochá. A tým, že sa guľatú Zem snažíme zobraziť na plochú mapu vznikajú nám matematické problémy. A o tom si povieme preto aj niečo viac.
Spôsob, ktorý sa využíva na zobrazenie zjednodušeného guľatého povrchu Zeme sa volá kartografické zobrazenie. Ide o jednoduché prenesenie trojrozmernej zemepisnej siete do roviny – do mapy prostredníctvom matematických a geometrických vzťahov. Tento vzťah rieši základný problém matematickej kartografie, a to akým spôsobom je možné rozvíjať guľovú plochu do roviny s čo najmenšími deformáciami. Na základe znalostí z matematickej kartografie tak následne môžu vznikať matematické konštrukcie, mapové projekcie, ktoré zachovávajú vybrané vlastnosti zemského povrchu tak, že skresľujú buď dĺžky, plochy alebo uhly.
V zásade tak vznikajú tri druhy mapových projekcií, rozlíšených podľa skreslenia:
- Rovnakouhlé (konformné) – zachováva uhly a tvary, pričom skresľuje plochy
- Rovnakoplošné (ekvivalentné) – zachováva plochy, avšak skreslenie uhlov sa prejavuje v tvare týchto plôch
- Rovnakodĺžkové (ekvidištančné) – zachováva dĺžky niektorej sústavy čiar (napr. zemepisných poludníkov, rovnobežiek) – táto projekcia nachádza využitie najmä v navigácii a orientácii
Druhým veľmi dôležitým kritériom je druh zobrazovacej (projekčnej) plochy. Tu rozlišujeme tiež tri druhy zobrazení:
- Rovinné (azimutálne) – obraz poludníkov tvorí zväzok polpriamok vychádzajúcich z obrazu pólu, rovnobežky sa zobrazujú do sústredných kružníc so stredom v obraze pólu
- Valcové (cylindrické) – obraz poludníkov a rovnobežiek sú úsečky rovnobežné s osou x, resp. y – príkladom je Mercatorove zobrazenie, ktoré zobrazuje polárne oblasti do obrovských rozmerov
- Kužeľové (kónické) – obraz poludníkov tvorí zväzok polpriamok vychádzajúci z vrcholu kužeľa a obraz rovnobežiek tvoria výseky sústredných kružníc
Týchto kritérií je samozrejme viacero – spomenúť ešte môžeme aj polohu zobrazovacej plochy alebo konštrukciu geografickej siete. Dôležitejšie je však výber kartografického zobrazenia so zreteľom na účel využitia mapy.
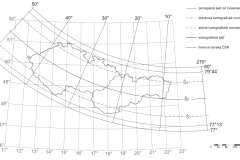
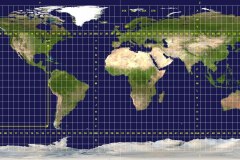
Kartografických zobrazení existuje aktuálne viac ako 300, v praxi sa však stretneme len s niekoľkými – najčastejšie to je Mercatorovo zobrazenie, prípadne pre Slovensko je zaujímavé spomenúť Křovákovo zobrazenie (konformné kužeľové zobrazenie – obr. 1). Veľká časť štátnych mapových diel v rôznych krajinách využíva aj Gauss-Krügerovo zobrazenie, neskôr nahradené zobrazením UTM (Universal Transverse Mercator – obr. 2). A na záver ešte spomenieme aj klasické azimutálne zobrazenie v stereografickej projekcii, ktoré je využívané najčastejšie pre polárne oblasti (Obr. 3). A práve toto zobrazenie je tak veľmi obľúbené pri zobrazovaní toho povestného, plochého zobrazenia, ktoré sme mohli vidieť aj v pamflete z roku 1849, neskôr aj v knižke (1865), od Samuela Rowbothama. Ale my už – narozdiel od pána Rowbothama vieme, že južný pól na našej guľatej Zemi (Obr. 4), naozaj existuje.
Obr. 1: Křovákovo zobrazenie (Krcho & Kuťková, Acta Geographica Universitatis Comenianae, 2010)
Obr. 2: Sieť zón zobrazenia UTM na elipsoide WGS 84 (wikimedia.org)
Obr. 3: Polárne oblasti - Arktída (Školský atlas sveta, VKÚ Harmanec, 2005)
Obr. 4: Polárne oblasti - Antarktída (Školský atlas sveta, VKÚ Harmanec, 2005)
Doplnkové čítanie a zdroj: Mičian et al. (1993). Geografia pre 1. ročník gymnázií, Slovenské pedagogické nakladateľstvo; Vajsáblová (2021). Matematické základy kartografie, Bratislava : Spektrum STU, 443 s., ISBN 978-80-227-5114-8.